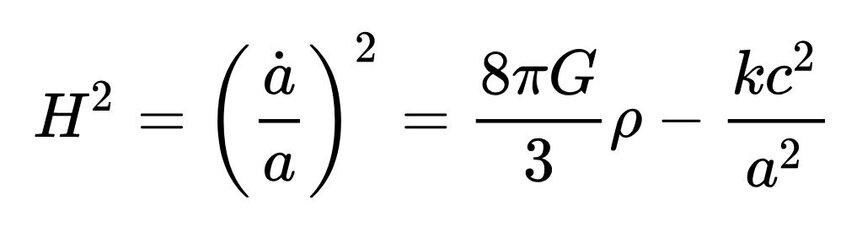Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
8 Things About Pi for Pi Day

Happy π Day!
Saturday is March 14, or, as it’s written in the U.S., 3/14. That makes it Pi Day, because the mathematical constant π is roughly equal to 3.14. Nerds celebrate this date every year, because, well, we’re nerds. Duh.
But this year’s π Day is special: It’s the year 2015, so the date is 3/14/15, giving us two more decimal places of the famous constant. In fact, if you celebrate it at 9:26:53 today, you get π to nine decimals: 3.141592653. Since the next digit is a 5, you can even round up and celebrate π Day for an extra second. Woohoo!
Why is π special? Most of us learn it because it’s the ratio of a circle’s circumference to its diameter. That’s pretty handy in geometry, but it goes much, much further than that. π appears in mathematical formulae all over the place, even where you might not expect it to. For some reason it appears to be woven into the very fabric of the Universe, popping up every time you look deeper into mathematics and physics.
In honor of this ubiquitous number, here are 8 (or 2π if you round down) facts about it you may or may not know. If you already know them, congrats! You’re a nerd. If not, then yay! You learned something. I can’t think of a better way to celebrate π Day than that.
A Year of π
Did you know there are different kinds of years? I won’t go into details (you can read all about them here, and I do mean all about them), but for our calendar we use what’s called a tropical year, which is 31,556,941 seconds long.
By coincidence, that is very close to π x 10 million! In fact, it’s off by less than half a percent. So if you need to know how many seconds there are in a year—which happens surprisingly often in my career— π x 10 million is a handy number to remember.
Legal π
There’s something of an urban legend that in 1897, Indiana tried to legislate the value of π to be exactly 3. That’s not precisely true. What happened was that an amateur mathematician had been working on a method to square the circle—to construct a square with the same area as a circle of given radius, using only a straightedge and a compass—and thought he found a solution (he hadn’t; there isn’t one). He submitted it to the Indiana Legislature, but it wasn’t ratified. His work didn’t even really say that π = 3; any value he found for π was incidental. But over the years, the story got warped, and now people think Indiana has that law in its books.
But that’s ridiculous. The government would never try to legislate a basic mathematical or scientific truth.
Anyway, there are other stories involved, like a joke story about Alabama redefining π, or the Bible stating it’s equal to 3. I find stories like this amusing. π is what it is, and humans trying to redefine it are, to coin an apropos phrase, trying to square the circle.
Pyramid π
When I was a kid, there was a huge industry in “ancient mysteries.” There still is, sadly—because I mean made-up mysteries, not real ones. Aliens didn’t help Hannibal cross the Alps, there’s no black hole in the Bermuda Triangle (the Bermuda Triangle doesn’t even exist), and the Egyptians didn’t really know about π.
Yeah, I’ve read quite a few breathless websites claiming they did. It’s even, they say, built into the pyramids! Well, one pyramid. Well, kinda. Basically, if you measure the circumference of the base of the Great Pyramid of Khufu and divide it by the height, you get a close approximation of 2π.
The thing is, that’s true! But it almost certainly wasn’t on purpose. It’s more likely to do with the slope of the wall chosen by the builders, which would drive the relationship between circumference and height. Also, many other pyramids (which had similar slopes) don’t have that same ratio, making it less likely to be mysterious ancient knowledge, and more a case of cherry-picking.
Mmmmm, cherry π picking.
π in Your i
Leonhard Euler was one of the greatest mathematicians of all time. He found a very weird relationship, called an identity, that goes like this: eiπ + 1 = 0. It’s a special case of a more generalized formula, but it’s true. e is the base of the natural logarithm, and i is the square root of -1, called an imaginary number (I’ll note it exists, in the sense that it has meaning in math, so the term “imaginary” is misleading).
This one simple formula has five of the most basic numbers in all of math in it, and they have this relatively simple relationship. Why is π in there? Well, the general equation has sines and cosines in it, and those have to do with circles, which is all about π! But the way it works out is still simple and elegant and beautiful. Also a bit mind-twisty. Actually, it’s a lot mind-twisty. But there you go.
20 πs
Another fun coincidence: eπ – π = 19.999099979. That’s really close to 20! I don’t think there’s any deeper meaning in that, though xkcd found a use for it. Hover your mouse over that cartoon and you’ll get another one, too.
Stubbing Your τ
Some people don’t like π. Or, to be more accurate, they think there’s a better number to use: τ, the Greek letter tau, which is equal to 2π. The reasoning behind this has to do with making equations simpler and more elegant, which is fine, but in the end I find it a bit of a wash. Replacing π with τ doesn’t really help you in the long run, and π is good enough. It’s a lot of fuss over what boils down to what seems like pedantry to me. And if we switch to τ we can’t make pie jokes! So that’s probably enough reason not to make the switch.
Slices of π
(This one’s mathy. If you’re a mathophobe, you might want to skip this, and if you’re an etymologist, don’t complain about the word mathophobe.)
So π turns up in lots of math equations. Part of that has to do with trigonometry, as I mentioned above; circles, sines, and cosines show up a lot. That means there are lots of ways to calculate π. You just have to manipulate the equation so you get π on one side, and all the messy formulae on the other. That kind of stuff has been around a long time, and if you’re curious, a Web search will keep you busy a while.
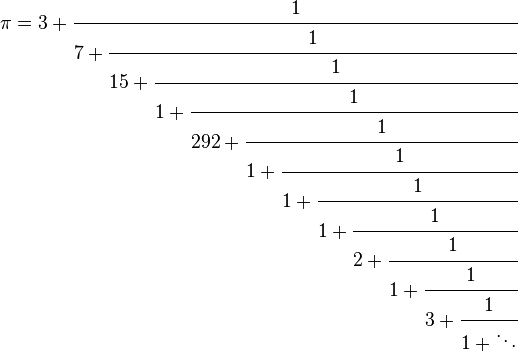
But I just found out about a new method—well, new to me—and it’s cool. It’s described by Evelyn Lamb at the Roots of Unity math blog. It has to do with what are called “continued fractions,” where you have a fraction inside another fraction. These are weird and a bit chewy to get your head around, but let me show you how this works. Here’s the fraction:
Yegads, I know. But we can break it down step by step, look at each part of the fraction and ignore the remainder until the next step.
So we start with the first part, which is 3. OK, good. That’s easy enough.
The next part is 1/7. That’s equal to 0.142857142857… If we cut the continuing fraction off there and add 3 to it, we’re already close to π: 3.142857…
The next part is 1/15. If we cut the fraction off there, then it’s 3 + 1/(7 + 1/15). That’s the same as 3 + 1/(106/15) = 3 + 15/106 = 3.1415094… which is a bit closer still.
If you keep doing that, following the fraction down, you get ever closer to π. As an armchair math nerd, this makes me smile. What’s interesting as well is that it converges quickly. After just two steps we’re already accurate to the fourth decimal! As Lamb points out, this makes it easier to memorize π if that’s your thing. In the case above, remembering three numbers (3, 7, 15) gets you to five digit accuracy. Doing the fraction means memorizing fewer numbers! Nifty.
The point? There’s more than one way to bake a π.
Universal π
Famous people born on π Day include astronauts Gene Cernan (1934) and Frank Borman (1928), and astronomer Giovanni Schiaparelli (1835).
But also, one Albert Einstein was born on March 14 in 1879. His equations for general relativity are still used today to describe the physical nature of the Universe, replacing Newton’s physics. This eventually led to what’s called the Friedmann equation, which describes the dynamics of the structure of space time:
Note the presence of π! Yes, it actually plays into the very fabric of space and time themselves! So no kidding, π is an important number. Carl Sagan uses this idea quite a bit in his fantastic novel Contact, too. The movie is great as well.
You might want to dismiss π Day as just a bit of silliness, but honestly, if there is a number we should pay our respects to, it’s π. It’s everywhere, and it’s not hard to make the case that our modern civilization depends on it (look around you; how many machined parts are circles, spheres, cylinders … and it pops up in equations governing electronics, too).
So have a happy π Day! And if you do celebrate it, make sure it’s with …
… a close circle of friends.
P.S. If you’re still not satiated with mathy days, have a look at my Mole Day article. I also wrote about Pi Day in 2013.
*Correction, March 13, 2015, at 13:45 UTC: This post originally misstated that eiπ–π= 19.999099979. The correct equation is eπ– π = 19.999099979.