Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
How do you know which pole of a planet is the *north* pole?

The problem with knowing a lot about astronomy — any subject, really — is what you think you know that you really don't.
To wit: the actor and comedian Dave Foley recently saw one of the magnificent Juno image of Jupiter's south pole, and asked a pretty salient question:
If you click that to read the thread, you'll see that someone "@-ed" me into it to see if I knew. I replied with the answer that I've always used:
But then @Dr Zig replied:
Hey! That was news to me! So I replied:
So what does all this mean? Here comes the science!
If you take a perfect sphere and just look at it, everywhere on its surface is exactly the same. They're all the same distance from the center, and that's their only defining characteristic. As a physicist might phrase it, there are no preferred (special) points on the surface. Every spot is just like every other spot.
But if you spin it, like magic (but science!) two special points appear: The poles. These are where the axis of rotation intersects the surface of the sphere. There are lots of ways to think of the poles; for example anywhere else on the rotating sphere, a point will make a circle in space as it moves around the rotation axis. But at the poles they don't. They just spin in place.
The two poles are different from each other in one way: If you look from above the surface down to one pole the sphere will appear to spin clockwise, and if you look down on the other pole it will appear to spin counterclockwise.
The Earth is a sphere, and if you were floating in space above the north pole the Earth appears to spin counterclockwise. From above the south pole it spins clockwise.
[Note: There is no up or down in space, so in these cases when I say "above something" I mean you have some altitude above the surface relative to the center of the Earth. It's easy to think of the north pole as up and the south pole down, but that's simply poleism (a word I just made up); it's an inherent prejudice because most people live in the northern hemisphere. If colonialism had started in, say, Australia, and spread across the world our maps would likely be upside-down relative to what we're used to.]
As it happens that's also true of most planets and the Sun, which is why I tweeted what I did. I thought the north pole was defined by the planet itself, but that's not the case!
The international Astronomical Union is the official Keeper of Names and Rules and Such™ for astronomy, and they have a definition for the north pole of a spinning object. It's actually defined using the Earth and Sun as its basis, so there are two steps.
One is that it uses the accepted location of the Earth's north pole, at 90° north latitude in the Arctic. OK, easy enough. But then they say that the north pole of another planet is the one that lies in the same celestial hemisphere relative to the invariable plane of the solar system as the Earth's north pole.
Okay, yikes. What does that mean?
First, we perceive the sky as a sphere around us, like we're seeing the inside of a huge spherical shell. That's actually a handy conceit! Because the Earth spins, it looks like the sky spins around us, making the stars rise and set. And that also defines a celestial north pole; the point in the sky directly above the Earth's north pole. It's also the point in the sky the stars appear to circle around. That means there's a celestial south pole and equator, too. We can even project the Earth's latitude and longitude up into the sky, creating a coordinate grid we call (for historical reasons) right ascension and declination. That way we can measure a star's coordinates on the sky just like you can give a city's coordinates on the surface of the Earth.
So any star north of the celestial equator is in the northern celestial hemisphere, just like any city north of the Earth's equator is in the northern hemisphere.
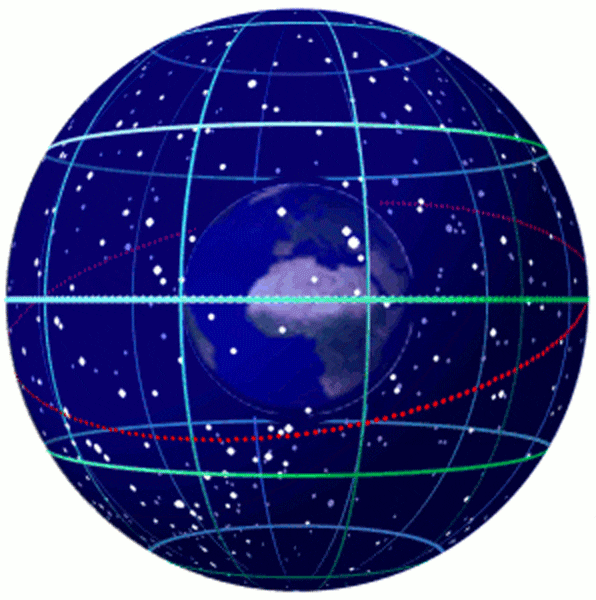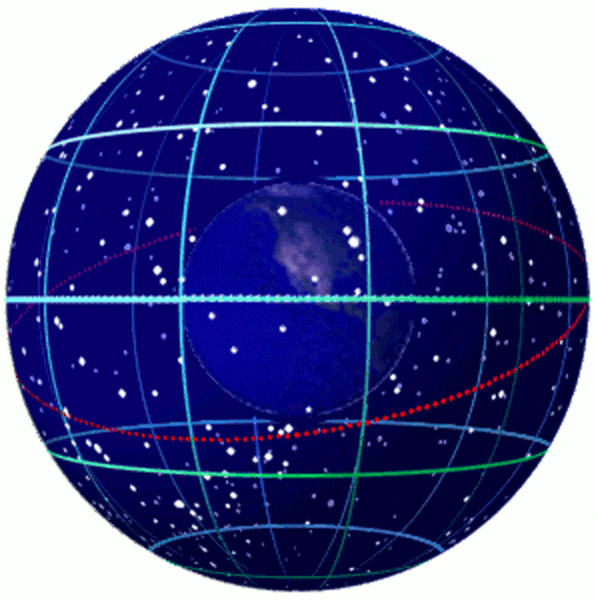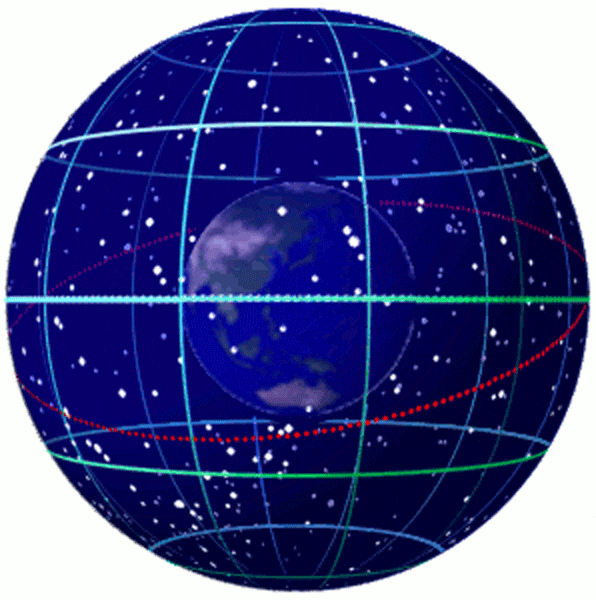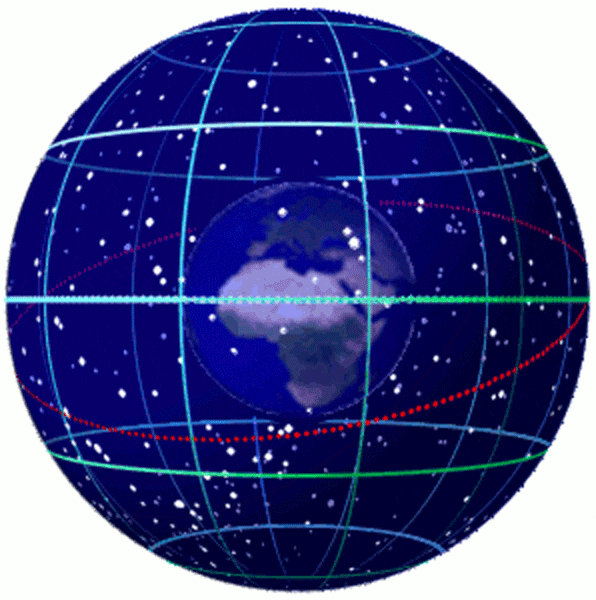
OK, so what's the invariable plane of the solar system? This is a clever way to set up a method to map things in the solar system. The solar system is three-dimensional, so we need to use three coordinates. But we also need an origin (the zero point) for that system, as well as a way to define the x-y plane.
Astronomers decided to use the total angular momentum of the solar system to define that plane. So what's that? It's a lot like the linear momentum you're familiar with. If an object is moving, it has momentum. There's a rigorous definition of it, but simply put it's the object's mass times its velocity. If you have two objects of the same mass but one is moving faster, it has more momentum. If you have two objects at the same speed but one is more massive, it has more momentum.
Angular momentum is like that, except it deals with the rotational momentum of an object. If you have two identical steel spheres, but one is spinning more rapidly, it has more angular momentum. This gets complicated, with some of it depending on the mass distribution inside a sphere, but we can ignore that here.
This is also true for systems of objects. The Sun has angular momentum because it spins, but the solar system itself has angular momentum because the planets orbit around the Sun (and they spin as well, though that's a small factor compared to their orbits). The orbits are all tilted relative to one another, but they all add to the system's overall angular momentum.
If you only had one planet orbiting the Sun, the plane of that orbit would define the plane of the angular momentum. With multiple planets at slightly different orbital tilts, though, they each contribute, altering that plane. The invariable plane is what you get when you add in all the contributions of all the planets (and moon, and asteroids and so on). Jupiter is the biggest contributor, but the other gas giants play a big role too.
If that's all a bit too much to handle (which I totally get!) then think of it this way: There is a way to define a plane that is like the equator of the solar system. It's mathy and complicated, but it's what we use, and we call it the invariable plane.
The invariable plane is very close to being the same as the Sun's equator, if that helps you picture it. Here's the important bit: We define "north of the invariable plane" as the hemisphere that contains the Earth's north celestial pole.
Now we're ready to get the IAU definition: The north pole of any planet is the pole that points toward somewhere in the north part of the sky relative to the invariable plane.
The Sun spins, and it has a pole that points into the northern part of the sky relative to the invariable plane, so that's the Sun's north pole. The same for any planet, moon, asteroid, comet, or what-have-you.
OK, as a definition I get it. But I don't like it.
Why? Because by that definition Venus and Uranus have north poles that point in the same direction as Earth's… but Venus and Uranus are flipped upside-down. We don't know why, but they are. So if you head out into space in the direction north of the invariable plane and look down on the planets, you'll see them all spinning counterclockwise, except Venus and Uranus.
Personally, that means to me that they are flipped upside-down. That in turn means their south poles point in the direction of our northern hemisphere. That makes sense to me.
But the IAU definition says no. Their north poles, by definition, point in the same hemisphere as ours does. That means they aren't flipped upside-down, it means they spin backwards.
It's may be a subtle point, but physically it's an important one. Flipping a planet over is hard, but it's WAY easier than stopping it and spinning it back up in the opposite direction (despite what Superman: The Movie would have you believe).
So for me, I'd rather define a planet's poles by the way it spins. If you're above its north pole it spins counterclockwise. That makes Venus and Uranus upside-down.
I'll note that I was researching this article I found out that in 2009 the IAU changed the rules for minor bodies in the solar system like asteroids, comets, and moon. The poles of these objects are defined by the direction of spin! Except instead of north and south poles, they call them the positive and negative poles. To define these, they use the "right hand rule": Curl the fingers of your right hand like you're cradling a mug of coffee. If the object spins in the direction your fingers are pointing, your thumb is the direction of the positive pole. If you think about it, that's exactly the same as my definition: Look down on the positive pole and the object is rotating counterclockwise.But that rule is just for minor bodies (they can have more complicated spins than planets, because they can flip over, tumble, and so on, changing their poles on short time scales). For planets, the IAU definition is independent of the direction of the spin of a planet. It says the planet's north pole is the one in the northern hemisphere of the sky as defined by the Earth.
That seems… self-centered.
But I get it. We need a definition, and that one works. I think mine's simpler, and less likely to cause confusion, but not causing confusion isn't a big motivation for the IAU, I sometimes think. Astronomers need some definition to make sure we're all on the same page, though, and with this definition at least, we are.
So I used those tweets as an excuse to write about this obscure but important rule, but to be honest all that esoterica isn't what I think people should take away from all this.
I walked into that Twitter conversation (invited!) and said what I thought was right, but wasn't. I learned something! That's cool. I love learning things, especially when it means I get to replace some faulty bit of knowledge with one that's accurate.
But even that's not what I want you to take away. Not some new knowledge, but instead this question:
How much do you think you know that you do know, and what do you think you know that you really don't know at all?