Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
How far away can you see a meteor?

I get email.
Most are asking questions of various types, most of which are fairly straightforward to answer (in fact, a lot could be answered by googling, hint hint). But sometimes I get a question that’s harder to answer, or even one that I’ve wondered about myself but never got around to figuring out.
So I was pretty intrigued when I got a question from Bad Reader Dean Lewis about meteors. During the Perseid meteor shower in 2018 he was away from his family, separated by about 1,000 kilometers. If he saw a meteor, was it possible they could see the same one from their more distant locale?
The short answer is: Yes! The long answer is… math. Cool, fun math.
And seeing as how, when this article is posted, the 2018 annual Geminid meteor shower peaks tonight, I think it's appropriate to figure this out.
If the Earth were perfectly flat, then in principle you could see a meteor all the way to any edge of the Earth. As long as you are above the ground, even a teeny bit, then your line of sight reaches every square centimeter of the planet on your side, so every meteor is visible to everyone. In reality, the air isn’t perfectly transparent, so at some distance you’re looking through so much muck you can’t see anything.
However, the Earth is not flat. Seriously! It’s round. And the atmosphere surrounds it like a shell, getting thinner with height and eventually petering out; that height depends on your definition of “space.” However, we can cheat a bit since we know science: Meteors like those in showers tend to burn up around 100 kilometers above the ground. That height depends on many things, including how big the meteoroids (the solid bits of interplanetary debris zipping through space) are, how fast they are moving, at what angle they enter the atmosphere, and so on. But let’s call it 100 km.
The closest a meteor can be to you is if you are directly under it, and then it’s 100 km straight up (at your zenith). If it burns up farther away from the zenith, then it must be farther from you. The farthest away you can see a meteor, it stands to reason, is therefore if it’s exactly on the horizon.
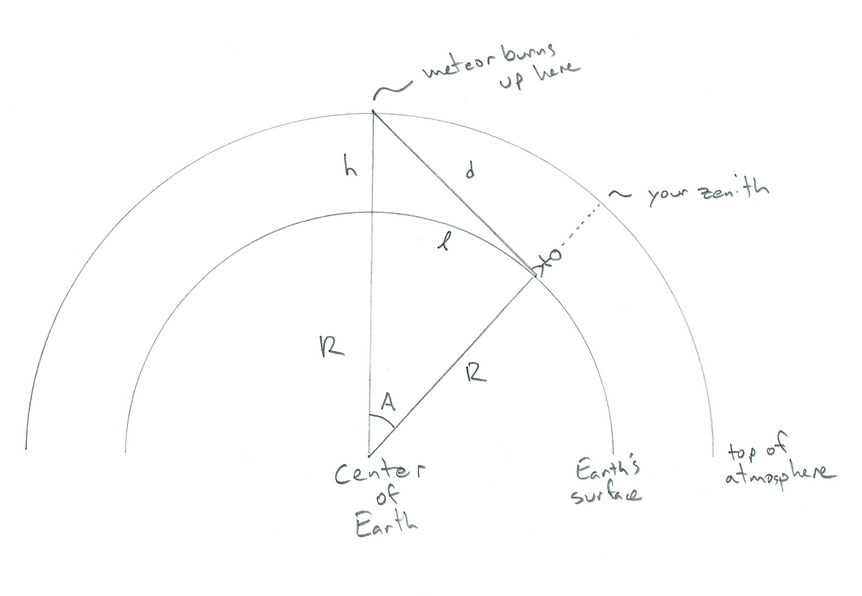
The geometry of it looks like this (note: NOT to scale):
You can see the little stick figure human standing on the surface of the curved Earth — let’s say that’s you — with the (also curved) atmosphere above them. In this diagram, R is the radius of the Earth (6,4000 km), h is the height the meteor burns up (100 km), and d is the distance from you to the meteor. A is the angle between your position on the Earth and the meteor’s position above it, and cursive l (as in length) is the distance you’d have to walk to have the meteor be directly overhead (I know that seems like a weird thing to want to know, but bear with me). Weirdly, you can calculate everything you need here without knowing d, but c’mon, it’s cool to know how far away the meteor is, right?
The key to all this is seeing that the angle between the meteor, you, and the center of the Earth is a right angle. That’s because the meteor is on the horizon as seen by you (or, if you prefer fun jargon, on the tangent line on the inner circle where R intersects it). That makes the triangle a right triangle, and if you remember your high school math, that means you can find all the sides and angles!
Remember the Pythagorean theorem? In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides*. In our triangle, the hypotenuse is R+h, and the other sides are R and d.
So
(R+h)2 = d2 + R2
or, multiplying out the left-hand side (use FOIL):
R2 + 2Rh + h2 = d2 + R2
Solve for d to see how far away the meteor is from you. Note that R2 is on both sides, so cancel them to get
d2 = 2Rh + h2
Or
d = square root(2Rh + h2)
Well, we know all those numbers! Plug-n-chug, baby:
d = square root(2 x 6,400 x 100 + 10,000) = 1,136 km
Aha! This means that if you see a meteor on the horizon, it’s over 1,100 kilometers away! That’s a long way, and technically the farthest away you can see a meteor from the ground.
Now let’s find cursive l. First we need to know the angle A. That requires some trigonometry. There are lots of trig identities you can use to figure this out, but my favorite† is that in a right triangle, the sine of an angle is the length of the opposite side divided by the length of the hypotenuse. So if we get that ratio, we can take the inverse sine (or arcsine) to get the angle.
sin(A) = d / (R + h)
so
A = sin-1(d / R + h)
Plug-n-chug again, and I get A = 10°. That’s a decent chunk of the Earth’s surface!
And now we can get cursive l. There are 360° around the Earth, and the circumference of the Earth is 2 x pi x radius = 40,192 km, so there are
40,192 km / 360° = 112 kilometers per degree
which means, in turn, 10° = 1,120 kilometers. That’s pretty close to d, which isn’t too surprising. The drawings are exaggerated, but in reality the shell of air over us is small compared to the size of the Earth. If I made the drawings to scale you’d see that d and l really are pretty close in length.
OK, so why am I all hot and bothered for finding l? Because of the original question! If you forgot after all that math, it’s how far away can two people be and still see the same meteor?
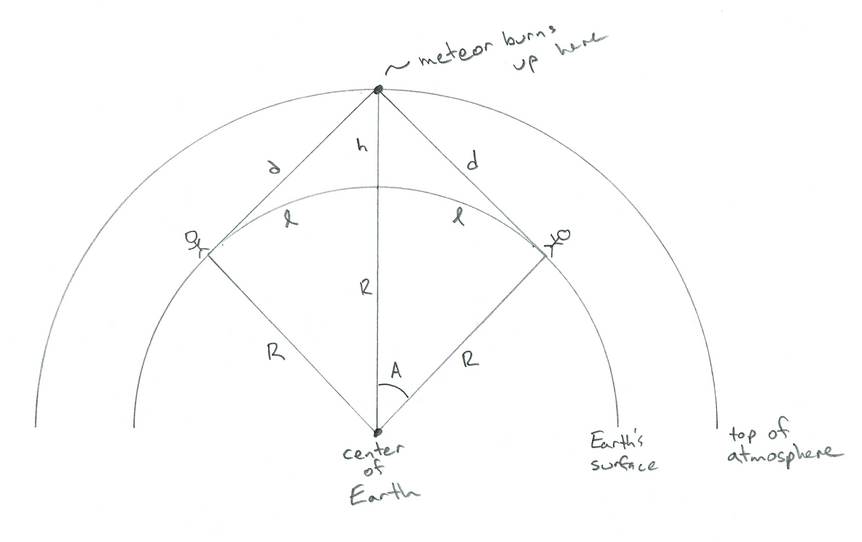
Well in that case the meteor would be directly between them, and on each of their respective horizons. That geometry looks like this:
AHA! Now you see why I want l! The distance between the two people is just 2 x l! So now we have the answer:
For two people to see the same meteor, they can be no more than 2 x 1,120 = 2,240 kilometers apart. As an example, that’s pretty close to the distance between Washington, DC and Denver. Wow.
Incidentally, for a change of perspective (literally), this means from the meteor’s viewpoint, it can see a stretch of Earth 2,240 kilometers wide (as in, DC on the eastern limb of the Earth and Denver on the western one). That’s pretty cool.
And that brings us to the actual answer to Dean’s question: If he was 1,000 km from his family, then yes, technically they could see the same meteor. How about that?
Now this again assumes the air is perfectly clear and all that, which in reality is essentially impossible. So this math represents an ideal situation (including the idea that the meteor is exactly between them).
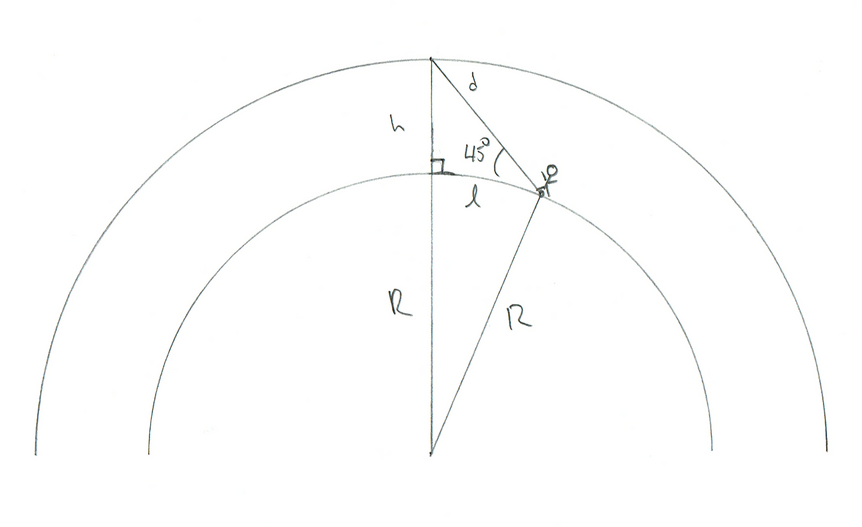
Let’s be more realistic. Let's say the meteor burns up in the sky at an altitude of 45° above the horizon for both observers. How far away would they be from each other? Well, again assuming the meteor is exactly between them, the geometry is more like this:
This is actually tougher to solve, but I know another trick: If we assume l is small, then the curvature of the Earth won’t be important. For example, if I want to know the distance between two trees in my yard, I don’t care that the Earth is curved. Over such a small distance I can assume it’s flat. Let’s make that assumption here.
In that case, we have another right triangle, but this time the right angle is the one under the meteor. I even labeled it in the diagram with the little square notation thingy. So if that’s a 90° angle, and our angle to the meteor is 45°, then the last angle (from the meteor to the observer) is also 45°. That means this must be an isosceles triangle, so l and h are the same! Since we know h is 100 km then so must l.
And that means the distance between our two observers is twice that, or 200 km.
Incidentally, in this case the distance to the meteor is about 141 km. I’ll leave confirming that as an exercise to the reader.
In principle, this means that if you know how high off the horizon a meteor is, and the altitude at which it burned up, you can calculate its distance (or if you know the distance you can get its height). That trig is pretty complicated, though, and I think I’ve thrown enough math at you for today.
But it’s cool to think that a little bit of high school math can have such a fun application. And I’ll admit it’s poetic and romantic to know that, as long as the separation isn’t too far, it’s possible to share seeing a shooting star with someone else. What a lovely thought.
*In The Wizard of Oz, the scarecrow got this wrong after he got a brain.
†Of course I have a favorite trig identity. What’s yours?