Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
Why don’t we see exoplanets sharing the same orbit? Tides.
Two planets that share the same orbit likely don’t exist.

Here’s something I’ve wondered about from time to time but never had an answer for: Why don’t we see two exoplanets sharing the same orbit?
Objects like this are called co-orbital, and we know they can exist for two reasons.
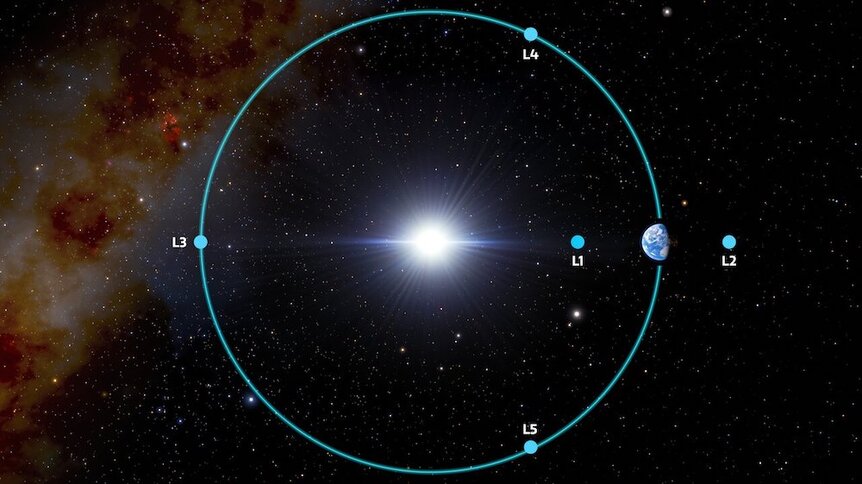
One is theoretical: When you solve the complex equations for the gravitational forces that exist around a small object like a planet orbiting a big object like a star, you find there are five regions of gravitational stability. These are like dips in the fabric of spacetime, where if you put something there they’ll stay there. These are called the Lagrange points, and are labeled L1 – L5.
Three of them — L1, L2, and L3 — are meta-stable, in that an object there can easily wander off under any kind of meager force, but L4 and L5 are much more stable. Even poking an object there won’t necessarily fling it away; it’ll settle back into place like a ball resting in the bottom of a bowl.
These two points are 60° ahead of a planet and 60° behind it in its orbit, and for historical reasons are called the Trojan points. Jupiter has a lot of asteroids in its Trojan points — NASA’s Lucy mission is already on its was to investigate them! — and Earth has at least one too. That’s the second reason we know co-orbital objects can exist: We see them in our own solar system. Even some moons of gas giants have Trojan asteroids sharing their orbits.
Yet, of the 5,000+ exoplanets known, no two have been found to share an orbit. It’s certainly possible; for example a gas giant planet with more mass than Jupiter has enough gravity that its L4 and L5 points could support an Earth-sized planet sharing its orbit. But none like this has been found.
It’s possible we missed some, since smaller planets are harder to observe, but still, having found exactly 0 really feels like the Universe is telling us that these orbits may not be as a stable as we think.
To see if that might be the case, a pair of astronomers investigated the physics of this. The mathematics behind this is complicated; for astronomers it’s usually something they learn in graduate school (I took a class on this during my time in grad school and it was, um, difficult) and even then the equations showing the existence of the Lagrange points is simplified. It leaves some forces out… in particular, tides.
The force of gravity that, say, a planet feels from a star depends on its distance from that star; gravity gets weaker with distance. But planets can be big objects, and the side closer to the star feels a slightly higher force of gravity than the side facing away. This change in gravity is what we call the tidal force.
This can have profound effects. The Moon orbiting the Earth feels tides from our planet that have moved it (and are still moving it) away from Earth, and locked the Moon’s rotation rate to its orbital motion. The Moon’s tides on Earth squeeze and stretch the planet, creating the more-or-less twice daily ocean tides, and are slowing the Earth’s rotation as well.
The astronomers looking into co-orbital exoplanets looked at the equations for the gravity in a three-body system of a star orbited by a big planet sharing an orbit with another, smaller planet. They solved these equations analytically (that is, going through the math) as well as using numerical simulations in a computer, and both agreed: Tides can destabilize a co-orbital object [link to paper].
The orbit of the small planet need not be exactly the same as the bigger planet; for example it could be a little more elliptical or tilted slightly. Ignoring tides, orbits like that can still be stable; the smaller planet would move around the L4 or L5 point but generally speaking stay in the same spot relative to the bigger planet. What the scientists found, though, is that the tidal forces tend to dampen those deviations, flattening the orbit of the smaller planet and making it more circular. That’s actually fine! That means in those cases tides tend to keep the object in an even more stable orbit.
However, there’s another case where the smaller planet’s orbit wobbles a bit, such that the object moves slightly ahead and behind the stable Lagrange point. Again, ignoring tides, such an orbit is generally stable. But what they found is that when they include tides, in many cases this type of oscillation, called a tadpole obit due its shape when graphed in a particular way, grows over time. The smaller planet eventually moves so far that it leaves the region of gravitational stability, and then its orbit changes so rapidly that it collides with the bigger planet or the star!
Yeah, that’ll tend to be a good reason we don’t see co-orbital objects. Slamming into a planet or a star does make continued existence difficult.
Their results are consistent with earlier work that was done in a different way, which means they’re likely right: Co-orbital planets are unlikely to exist for very long. It can work when the third object is very small like an asteroid, but once it gets large enough to have strong enough gravity, the system becomes unstable pretty quickly, cosmically speaking.
So it appears that co-orbital planets may not exist. The proof is in the observations, though; while we haven’t seen one yet that doesn’t mean they’re not out there. Still, the fact that after 5,000 exoplanets seen and none is co-orbital is telling us that at best the situation is rare.
That’s too bad! It’s a staple of sci-fi, and it would make space travel to other worlds a lot easier; you need a lot less fuel to get to an object sharing your own orbit. I’ll note there are systems where the planets are still pretty close together, like TRAPPIST-1, and they may even be really common, so that’s still pretty nifty. But two planets sharing an orbit may be something we really only will see in fictional tales.