Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
Seeing Einstein's hand in stars orbiting a supermassive black hole

Sitting in the middle of our Milky Way galaxy is a monster black hole. And by “middle,” I mean the exact center of the galaxy; it probably formed at the same time as the galaxy, itself, billions of years ago, and grew large as the galaxy did, too. It sits right there at the core, like a drain in the middle of a vast bathtub, mostly minding its own business but occasionally eating the odd star or gas cloud.
We think every big galaxy has one of these supermassive black holes in their hearts. Mostly, those are detected because they have disks of gas swirling madly around them, and observations can detect the motion of the gas via the Doppler shift as it orbits (we don’t usually see the disks themselves, which are too small).
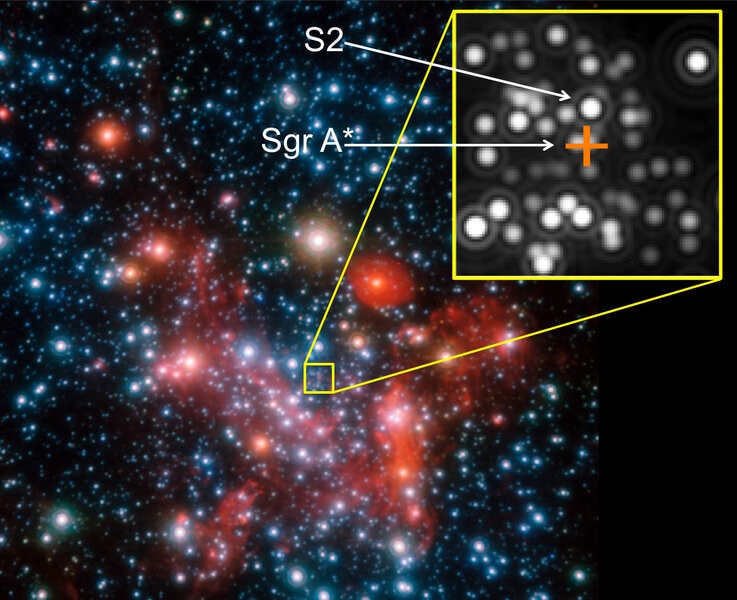
But our galaxy is different. We’re in it, so we’re close to the black hole, and we have a better view. Not too close; we’re still halfway out to the edge of the galaxy, so we’re safe! But there are a few dozen stars that orbit the black hole far more closely, and because of our closer seat we can actually see them move as they do!
As an aside, this is one of the all-time coolest things I know about astronomy. It takes the Sun over two hundred million years to circle the galaxy once, but these stars are so close to the center, so close to the black hole, that they only take decades. That means that we can literally see them move year after year:
Scientifically, this is a very big deal. We’ve known for centuries that if you can observe an object orbiting a more massive object, you can calculate the mass of that second object. If you know the first object’s orbital velocity (how fast it’s moving as it goes around) you can also calculate the distance to them.
So, if we observe the stars orbiting that black hole in the center of the Milky Way (astronomers call it Sgr A*, literally pronounced “Sagittarius A star” or “Saj A star” if you feel more informal about it), we can, in principle, figure out the mass of the black hole and our distance from it.
Not that that’s easy...but it’s been done. Powerful telescopes observing in the infrared (to make it easier to see the stars through all the dust and muck toward the center of the galaxy) have been able to watch these stars in their orbits, and also measure their Doppler shifts. That gives their velocities, too.
Using this method, we’ve been able to measure the mass of the black hole as being around 4 million times that of the Sun, and its distance as about 26,000 light years.
As amazing as that is, a team of astronomers decided they might be able to do more.
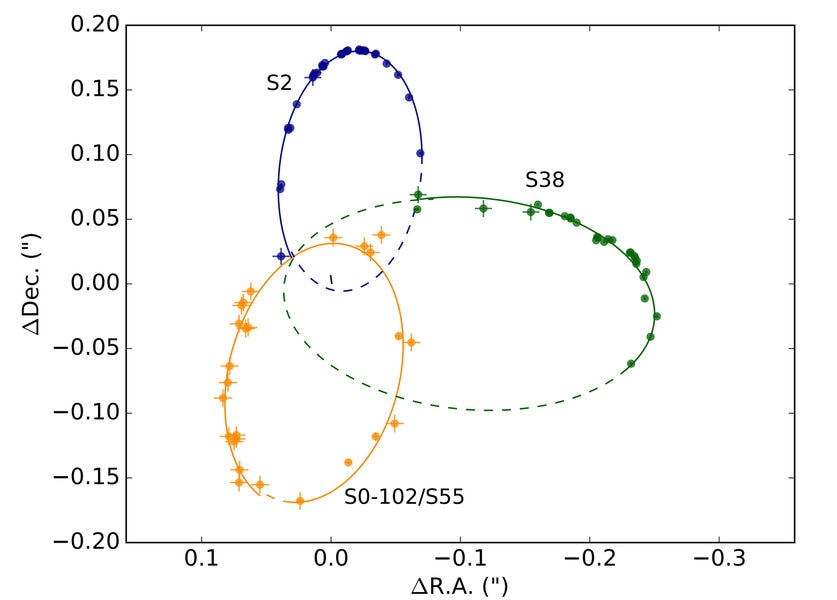
One of the stars orbiting the black hole is called S2. Its orbit brings it pretty close to Sgr A*, a hair-raising 18 billion kilometers, the equivalent of four times the distance from the Sun to Neptune. When it’s at that point in its orbit it’s screaming through space at the colossal speed of 6000 kilometers per second, 0.02 times the speed of light.
This is so close to the black hole that Einsteinian relativistic effects can kick in. There are quite a few, but one, in particular, is very interesting. If an object is in an elliptical orbit around something massive, the orientation of that ellipse will rotate over time. In other words, if you draw a line through the long axis of the ellipse, that line will rotate a little bit every time the object orbits. The effect is strongest at periapsis, the point when the orbiting object is closest to the object it orbits.
We actually have measured this effect; Mercury’s orbit does this. The effect is tiny, and difficult to measure, because the Sun isn’t very massive (in the relativistic sense) and mercury doesn’t get that close. But we do see it, and it’s exactly as Einstein’s equations of General Relativity predict.
This new team of astronomers thought that perhaps they could see this effect as the star S2 orbits Sgr A*. They looked at the observational data from 2002 (when S2 was last at periapsis) to 2015 and found that S2 maybe, barely, shows this effect. Their results certainly are at least consistent with what Einstein predicted.
That’s amazing. This has never been seen on this scale, before. And while their results are a touch iffy, we’ll know better soon enough: S2 reaches periapsis once again sometime between April and July 2018 (the orbital characteristics aren’t perfectly known, so there’s a bit of uncertainty there). During that time, telescopes will be peering intently at the center of our galaxy, very carefully measuring the position of the star.
...and a few others. S2 is just the nearest bright star to Sgr A*. There’s another that’s closer but fainter, and harder to get accurate positions for it, but quite a few other stars have been seen orbiting the black hole as well. The team looked at them too, and by calculating their orbits were able to narrow down the mass and distance to the black hole: 4.15 million times the mass of the Sun, and at a distance from us of 26,700 light years (with some small uncertainties).
Again being able to do this is, quite simply, incredible, in the awe-inspiring sense of the word. Scientifically, it’s amazing enough; we know that there are characteristics of these supermassive black holes that seem to correlate with the galaxy around them (the way stars orbit the center, for example, seems to scale with the mass of the black hole), so being able to nail down the mass and distance our own local supermassive beastie is stunning.
But the fact of the matter is that it’s astonishing that we can do this at all. This is a ridiculously finicky set of observations coupled with ridiculously complicated mathematics describing the overall shape and character of space itself.
Yet, we can make these observations, and we can apply that math, and we can couple them to discover what a hole in spacetime 260 quadrillion kilometers away is doing as it tosses around multiple-octillion ton stars.
Why do we do this? Because we’re curious. Because we’re smart. Because we want to discover, and, most importantly, to understand.
This has driven us to investigate the Universe, itself...and to know our place in it.