The Sunburst Arc: A quirk of gravity reveals how the infant Universe lit up

It’s difficult to describe the immensity of galaxy clusters; they are among the biggest coherent structures in the Universe (what’s bigger? Superclusters, which are clusters of clusters!). Imagine a collection of, oh, say, a thousand galaxies the size of the Milky Way. The sky inside one must be incredible! So many galaxies you could see with your naked eye…

From Earth we see them from far away, though, and study them avidly. They tell us a lot about the Universe on its grandest scales, and sometimes they also tell us about what it was like when it was young. That’s due to gravitational lensing, a peculiar effect of relativity where the overall gravity of the cluster bends the light of an even more distant galaxy behind it, distorting it and making it brighter.

We’ve seen this many times before, but a recent discovery is very cool: The brightest lensed galaxy ever seen, bent into four different arcs, for a total of twelve separate images of the same galaxy!

A cluster of galaxies 4.6 billion light years away acts like a lens, distorting, magnifying, and multiply replicating an image of a more distant galaxy 11 bilion light years away into a series of arcs. Credit: ESA/Hubble, NASA, Rivera-Thorsen et al.

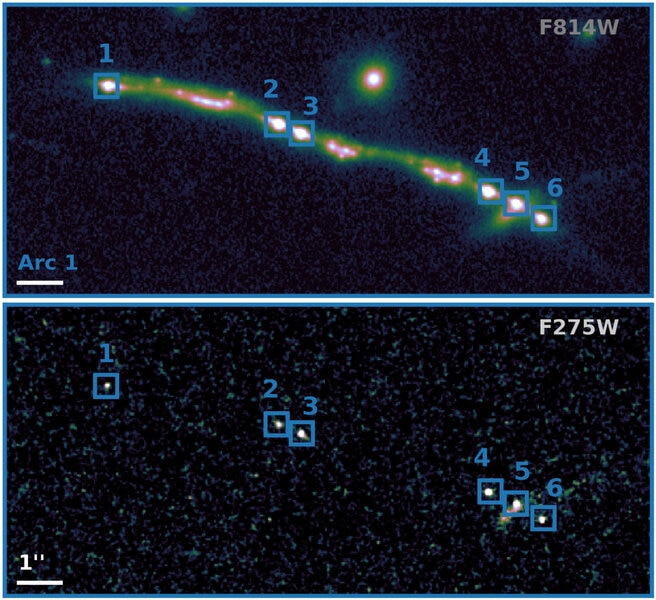
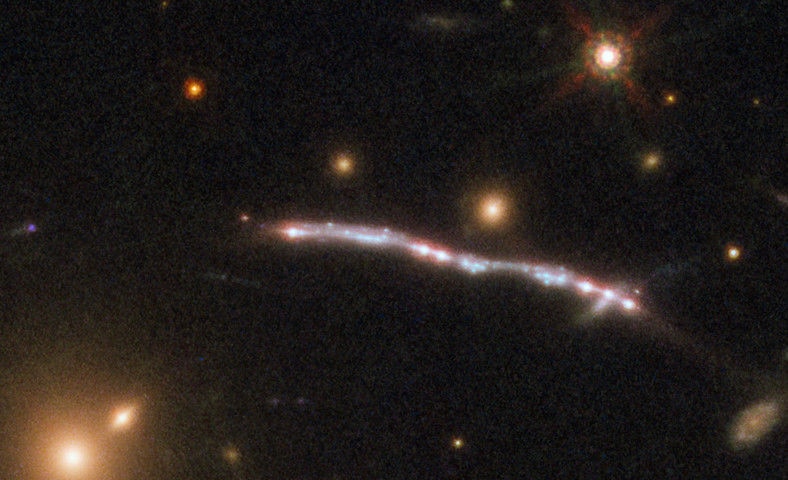
Whoa. The cluster is called PSZ1 G311.65−18.48, and the lensed galaxy is PSZ1- 36 ARC G311.6602–18.4624 (no wonder the astronomers nicknamed it the Sunburst Arc, which I think I will use as well). You can see three arcs above and to the right of the cluster core, and the fourth is down and to the left, partially obscured by a foreground star. Each arc is that same background galaxy — in fact, in the upper arc the six bright “stars” along its length are images of the same small region inside the galaxy, multiplied by the distorted gravity of the cluster! And that turns out to be very interesting indeed.

That small bright spot in the Sunburst Arc is actually a star-forming region: A cloud of gas and dust actively forming stars. Given how big it is in the image, and accounting for the magnifying effects of the gravitational lens, it’s less than 500 light years across, comparable to big, bright nebulae in nearby galaxies.

Detail of one Starburst Arc shows several bright knots; each is an image of the same region of the lensed galaxy replicated through the lensing process. Credit: ESA/Hubble, NASA, Rivera-Thorsen et al.

Here’s where things get fun. The cluster of galaxies is about 4.6 billion light years from us, but the galaxy forming the Sunburst Arc is much more distant, about 11 billion light years away. The light we see from that galaxy is therefore coming from when it was very young, just 2.8 billion years after the Big Bang! Things have changed a lot in the Universe since then, so this galaxy is in many ways analogous to even younger galaxies.

That presents an opportunity. Not long after the first stars formed, the Universe underwent a key event called reionization, when high-energy ultraviolet light from the first stars was able to fight its way out of the thick gas and dust inside the galaxy and zap the material in between galaxies. That material was opaque, but the light from these stars was so fierce (these first generation stars could grow to incredibly massive sizes, and were staggeringly luminous compared to stars today) it ionized the atoms (ripped the electrons off the atomic nuclei). The problem is, those stars are so distant — they’d be over 13 billion years away from us — it’s hard to study this event.

It’s not clear just how that light escaped those galaxies. Was it because the interstellar gas and dust was patchy, allowing leaks of UV light? Or was the gas in a thick shell, with channels in it that allowed light through? These two ideas predict different amounts of light getting out as well as different sized regions it escapes from. That’s where these new observations come in. The astronomers used two different filters with Hubble, one to look at the ionizing radiation (by the time it gets to us, that far-UV light is redshifted to near UV, right into the wavelength range of one of Hubble’s many filters), and another to look at non-ionizing light also emitted by the galaxy. By comparing the two they can constrain where the light is coming from and how much is escaping.

The top arc is actually the same galaxy replicated six times. The long-wavelength filter (top) shows the bright knot plus underlying stars in the galaxy, while the short-wavelength filter (bottom) picks out just the UV light from the knot. Credit: Adapted from Rivera-Thorsen et al.

What they found is that the Hubble images look almost exactly like what you’d expect from a perforated shell, a thick shell with channels going all the way through it. And that lends credence to the idea that this is how things worked even earlier in the life of the Universe, when those first stars were lighting up the cosmos.

While this may seem a bit subtle and even esoteric, this is an important result! It distinguishes between two competing ideas of how the gas was distributed in the very early Universe, and that in turn tells us a lot about things like what galaxies looked like in the very early days (and maybe even before galaxies themselves formed as discrete structures), how those first stars were born and lived their lives, and on a bigger scale how the Universe itself was structured when it was an infant.

Mind you, there’s a clear chain of circumstances from then to now, with some overlap between steps. Big Bang, inflation, first stars, reionization, galaxy formation, more normal stars started forming, stars like the Sun formed, they formed planets around them, one of them had life start on it, evolution worked its wonders, and now you’re reading these words. Every step in this process is affected by the one before it, so you literally owe your existence to the way the gas in the early Universe was distributed.

And now, thanks to a weird quirk of relativity and gravity, we can see that.  

Esoteric? Sure. Important? Absolutely. And another piece of the literally cosmic puzzle is put into place, making the picture clearer.