Create a free profile to get unlimited access to exclusive videos, sweepstakes, and more!
How do you calculate the orbit of an object in space?
On the blog recently I wrote about 20 new moons of Saturn that were just discovered. Finding them was hard, since the astronomer had to go through images by eye to look for very faint moving objects.
But once he found them, he was able to predict their positions in the future, and look for them in later images. It worked, and the moons were made official.
But how did he do it? By carefully measuring their motions, he could trace their paths around Saturn, their orbits. Given enough observations, the ellipse each makes around the planet can be determined pretty well. An ellipse is a shape with very specific characteristics, and these can be defined mathematically — Johannes Kepler figured this out in the 17th century!
For a given ellipse, only a handful of numbers are needed to define its shape, size, and orientation in space. If you have that, plus where the object was located in its orbit at a given time, you can use the equations of motion of a body under the influence of another body’s gravity to predict where the object will be in the future! And postdict (the opposite of predict) where it was in the past, which can be useful too.
The more observations you make over time, the better you define that ellipse and motion, and the more confident you can be in determining its location in the future or past (I describe how this works in an earlier article). If you can get the numbers accurate enough, you might find the object was observed by another telescope in the past just by happenstance. You can then find that image and use it to greatly extend your baseline of observations, allowing even better determination of those ellipse-defining numbers (this is a big advantage of digital imaging in astronomy, since we can save observations to a database; many asteroids and comets have been found in older images this way).
Mind you, it’s not like this is easy! The equations needed to do this are… daunting. When I was an undergrad we had a homework assignment: We were given the list of variables describing an asteroid's orbital ellipse, and a photo of a big area of the sky with a bazillion stars in it, as well as, somewhere in there, the asteroid. Given the coordinates on the sky (like latitude and longitude on Earth) of the center of the photograph, and the date it was taken, our task was to find the asteroid in the photo. We had to apply those equations to the variables given, and work through the math. I’ll gently remind you that I am not exactly young, so this was before computers were readily available to do this kind of tedious gruntwork.
So, like generations of astronomers before me, I sat on the floor of my dorm room with a pencil and a tablet of paper, started writing out the equations, and started propagating all the numbers through. I had a calculator which made it possible, but I had to write down hundreds of numbers, meaning transcription errors were likely, and I had to triple-check everything, and and and. It took all weekend, but I got an answer. I checked it and rechecked it, and I could swear I did everything right.
Translating my results to the photo and calculating its position, I found the asteroid to be… about four inches off the edge, outside the photo. ARRRRRGGGGGGGG!
However, I distinctly remember getting the closest answer of anyone in the class! So I was the least wrong.
OK, anecdote aside, how does this work? What are these numbers you need?
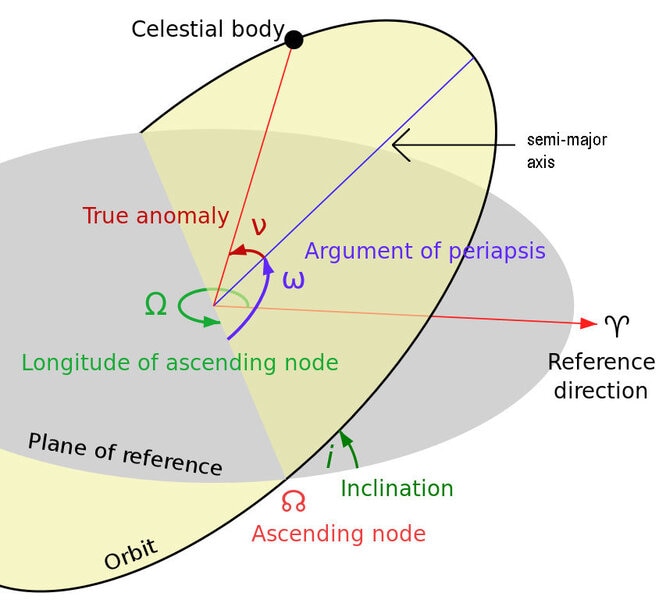
They're called the Keplerian orbital elements, and there are six of them. First, the length of the ellipse across its widest dimension. This is called the major axis, and what you really need is that divided in half, called the semi-major axis. You also need the eccentricity, which is how much the ellipse deviates from a circle, from 0 to 1 (an eccentricity of 0 is a circle, and 1 is no longer an ellipse, it's a parabola, so technically the longest ellipse you can have would have an eccentricity of 0.999999…).
So that’s the shape of the ellipse. For its orientation in space, you need to define some reference plane, like say the equator of the object it’s orbiting. Then your ellipse is tilted to that by some amount, called the inclination. This defines two points, called nodes. At one node the object is moving up relative to your reference plane, and the other one it’s moving down. These are called the ascending and descending nodes. The orbital ellipse can be rotated around your reference plane, too, so you look at the angle between the ascending node and some reference point on the sky (sometimes called the vernal point) and call that the longitude of the ascending node. That angle tells you how much it's rotated.
Finally, there are two more. One is called the argument of periapsis — I love all these terms, they're so old fashioned and fancy. Steampunky. Anyway, periapsis is where the object is closet to the body it orbits (or if you prefer when it's at the the short leg of the major axis). The argument of periapsis is the angle between that point on the orbit ellipse and the reference plane.
The other is called the true anomaly, and it’s the object’s position along the orbital ellipse at a given time, measured from periapsis.
Simple, right?
I know, your head is probably spinning around in an ellipse. But I found a video that explains each of these and it does a good job showing you what each element means:
So, once you have all the specific orbital elements, you can plug them into the equations (when they’re properly formulated, which is a whole 'nuther can o' worms… and I'll note that getting these elements in the first place from observations is also a tricky business) and it’s off to the orbital races! Of course, nowadays you whippersnappers with your iPads and your tablet phones and your apps: You can use a computer to do all the ridiculously hard math. In fact, once you have the orbital elements, you can just plop them into the code and crank out predictions of the object’s positions I the past and future all you want.
This is actually what inspired me to write this! After I wrote about the new moons of Saturn, I was talking about them on Twitter, and Ian Webster, a software engineer, tweeted this:
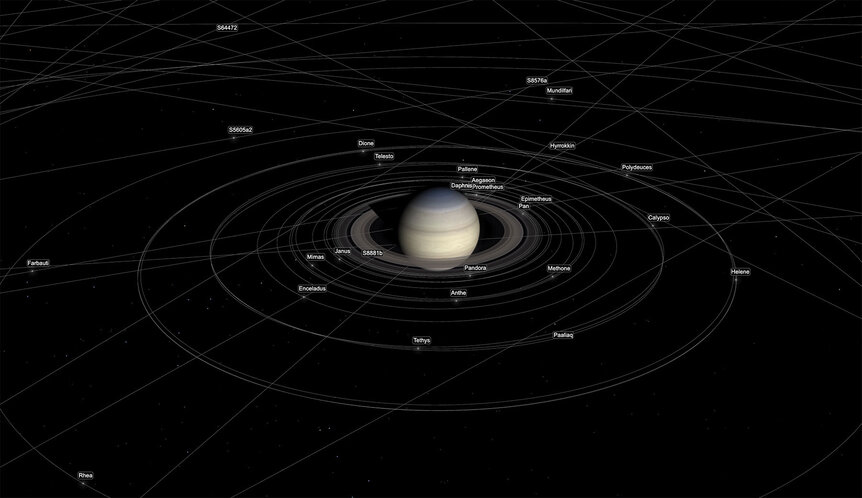
Whoa. I immediately went to the page linked and started playing around. It's very, very cool. You can display all of Saturn's moons, tilt and zoom, highlight different orbits, and more. It's pretty intuitive. Pan out, set the timer to move quickly, and watch the outer moons zipping around!
Here's the thing: He posted that just a few days after those moons were announced! That’s the power of Keplerian orbital mechanics: Once you have those equations programmed into a computer, all you need to do is add the orbital elements to the code (well, to a database, I'm guessing, that's read by the code) and boom! You can watch them orbit their planet.
And it works for other planets, too, like Jupiter. It's amazing. And I'll admit: I knew Saturn had 82 moons, and Jupiter 79, but I hadn't internalized what that actually looked like. Now I don't need to. This software shows me.
Things have come a long, long way since I sat on my dorm room floor in despair. Or when Kepler had to do all the math by hand. At least I had a calculator.